Predicting Heart Disease using Machine Learning

This notebook will introduce some foundation machine learning and data science concepts by exploring the problem of heart disease classification.

It is intended to be an end-to-end example of what a data science and machine learning proof of concept might look like.

What is classification?

Classification involves deciding whether a sample is part of one class or another (single-class classification). If there are multiple class options, it's referred to as multi-class classification.

What we'll end up with

Since we already have a dataset, we'll approach the problem with the following machine learning modelling framework.
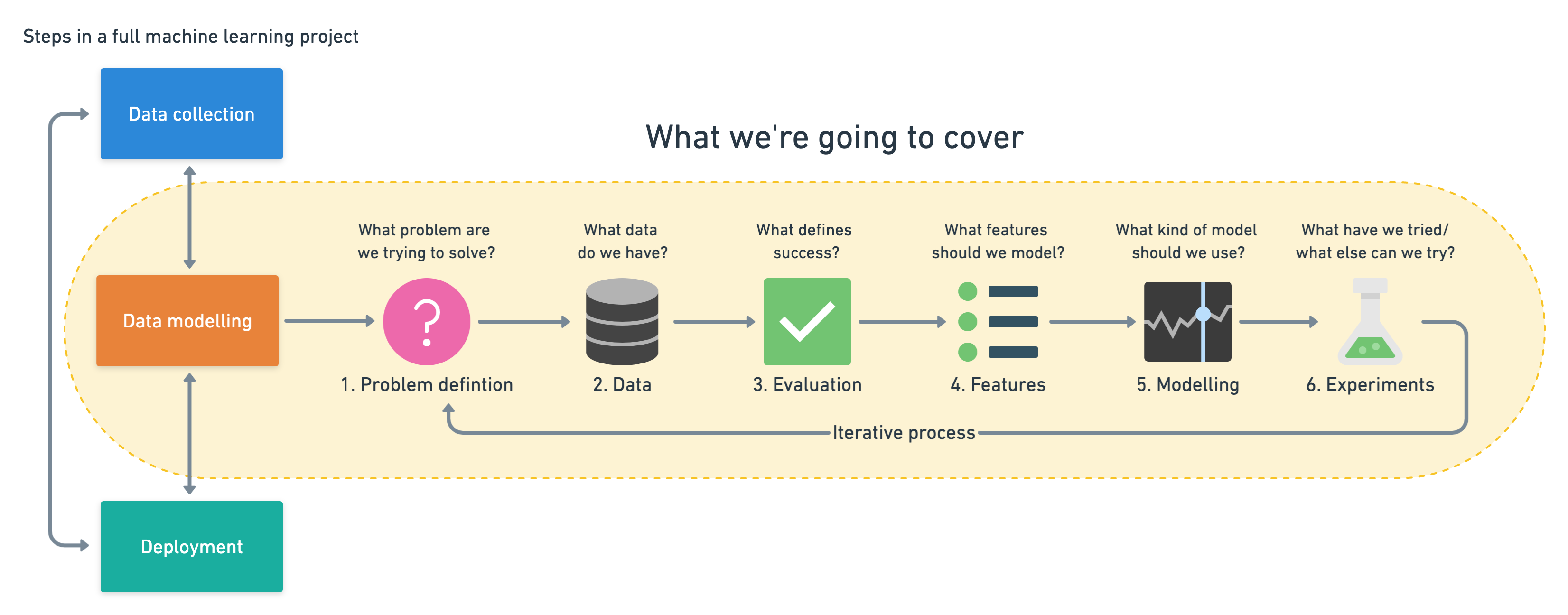6 Step Machine Learning Modelling Framework

More specifically, we'll look at the following topics.

To work through these topics, we'll use pandas, Matplotlib and NumPy for data anaylsis, as well as, Scikit-Learn for machine learning and modelling tasks.
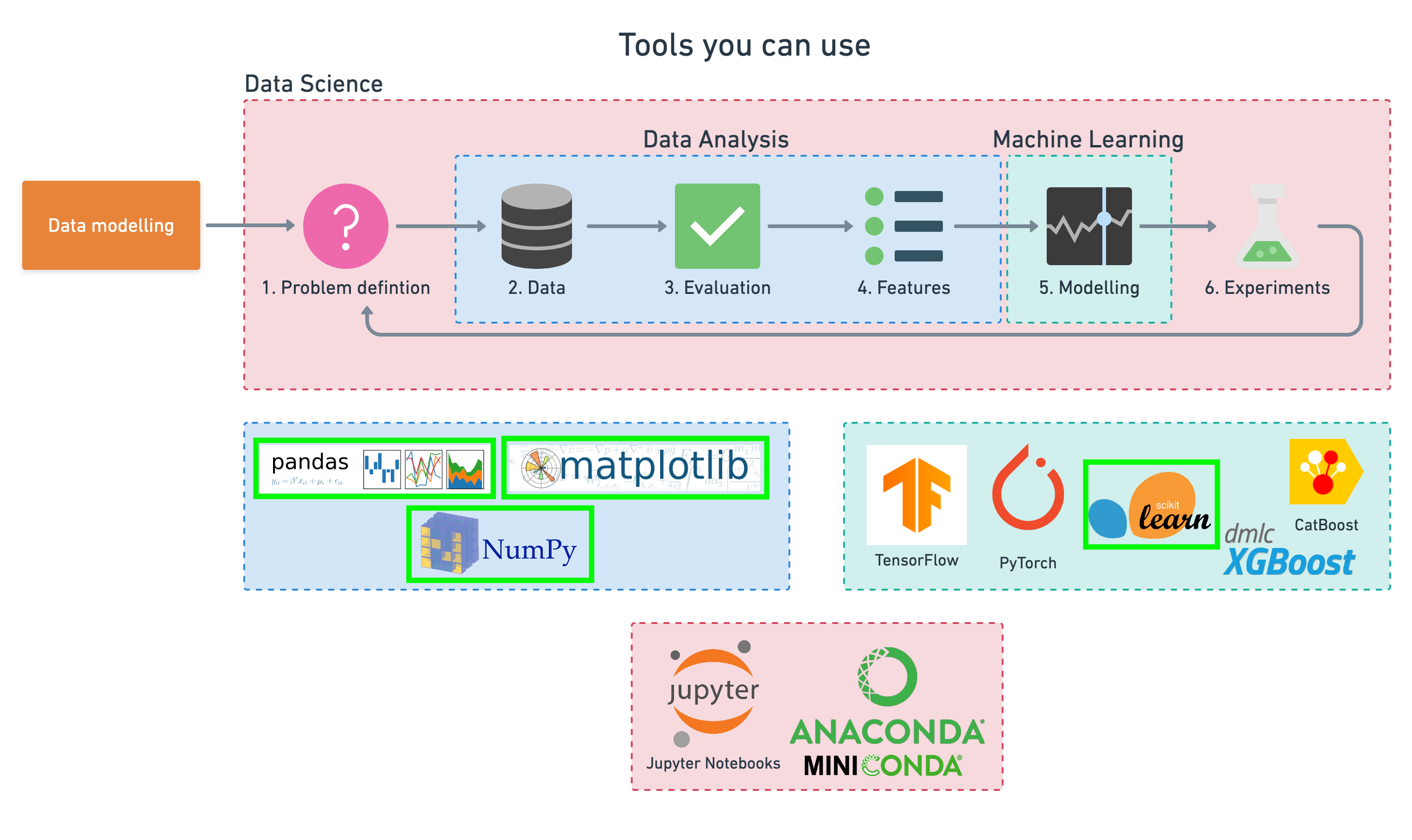Tools which can be used for each step of the machine learning modelling process.

We'll work through each step and by the end of the notebook, we'll have a handful of models, all which can predict whether or not a person has heart disease based on a number of different parameters at a considerable accuracy.

You'll also be able to describe which parameters are more indicative than others, for example, sex may be more important than age.

1. Problem Definition

In our case, the problem we will be exploring is binary classification (a sample can only be one of two things).

This is because we're going to be using a number of differnet features (pieces of information) about a person to predict whether they have heart disease or not.

In a statement,

Given clinical parameters about a patient, can we predict whether or not they have heart disease?

2. Data

What you'll want to do here is dive into the data your problem definition is based on. This may involve, sourcing, defining different parameters, talking to experts about it and finding out what you should expect.

The original data came from the Cleveland database from UCI Machine Learning Repository.

Howevever, we've downloaded it in a formatted way from Kaggle.

The original database contains 76 attributes, but here only 14 attributes will be used. Attributes (also called features) are the variables what we'll use to predict our target variable.

Attributes and features are also referred to as independent variables and a target variable can be referred to as a dependent variable.

We use the independent variables to predict our dependent variable.

Or in our case, the independent variables are a patients different medical attributes and the dependent variable is whether or not they have heart disease.

3. Evaluation

The evaluation metric is something you might define at the start of a project.

Since machine learning is very experimental, you might say something like,

If we can reach 95% accuracy at predicting whether or not a patient has heart disease during the proof of concept, we'll pursure this project.

The reason this is helpful is it provides a rough goal for a machine learning engineer or data scientist to work towards.

However, due to the nature of experimentation, the evaluation metric may change over time.

4. Features

Features are different parts of the data. During this step, you'll want to start finding out what you can about the data.

One of the most common ways to do this, is to create a data dictionary.

Heart Disease Data Dictionary

A data dictionary describes the data you're dealing with. Not all datasets come with them so this is where you may have to do your research or ask a subject matter expert (someone who knows about the data) for more.

The following are the features we'll use to predict our target variable (heart disease or no heart disease).

  1. age - age in years
  2. sex - (1 = male; 0 = female)
  3. cp - chest pain type
    • 0: Typical angina: chest pain related decrease blood supply to the heart
    • 1: Atypical angina: chest pain not related to heart
    • 2: Non-anginal pain: typically esophageal spasms (non heart related)
    • 3: Asymptomatic: chest pain not showing signs of disease
  4. trestbps - resting blood pressure (in mm Hg on admission to the hospital)
    • anything above 130-140 is typically cause for concern
  5. chol - serum cholestoral in mg/dl
    • serum = LDL + HDL + .2 * triglycerides
    • above 200 is cause for concern
  6. fbs - (fasting blood sugar > 120 mg/dl) (1 = true; 0 = false)
    • '>126' mg/dL signals diabetes
  7. restecg - resting electrocardiographic results
    • 0: Nothing to note
    • 1: ST-T Wave abnormality
      • can range from mild symptoms to severe problems
      • signals non-normal heart beat
    • 2: Possible or definite left ventricular hypertrophy
      • Enlarged heart's main pumping chamber
  8. thalach - maximum heart rate achieved
  9. exang - exercise induced angina (1 = yes; 0 = no)
  10. oldpeak - ST depression induced by exercise relative to rest
    • looks at stress of heart during excercise
    • unhealthy heart will stress more
  11. slope - the slope of the peak exercise ST segment
    • 0: Upsloping: better heart rate with excercise (uncommon)
    • 1: Flatsloping: minimal change (typical healthy heart)
    • 2: Downslopins: signs of unhealthy heart
  12. ca - number of major vessels (0-3) colored by flourosopy
    • colored vessel means the doctor can see the blood passing through
    • the more blood movement the better (no clots)
  13. thal - thalium stress result
    • 1,3: normal
    • 6: fixed defect: used to be defect but ok now
    • 7: reversable defect: no proper blood movement when excercising
  14. target - have disease or not (1=yes, 0=no) (= the predicted attribute)

Note: No personal identifiable information (PPI) can be found in the dataset.

It's a good idea to save these to a Python dictionary or in an external file, so we can look at them later without coming back here.

Preparing the tools

At the start of any project, it's custom to see the required libraries imported in a big chunk like you can see below.

However, in practice, your projects may import libraries as you go. After you've spent a couple of hours working on your problem, you'll probably want to do some tidying up. This is where you may want to consolidate every library you've used at the top of your notebook (like the cell below).

The libraries you use will differ from project to project. But there are a few which will you'll likely take advantage of during almost every structured data project.

Load Data

Data Exploration (EDA)

The goal here is to find out more about the data and become a subject matter export on the dataset you're working wit.

  1. What question(s) are you trying to solve?
  2. What kind of data do we have and how do we treat different types?
  3. What's missing from the data and how to deal with it?
  4. Where are the outlines and why should you care about them?
  5. How can you add, change or remove features to get more out of your data?

Heart Diseae Frequency according to Sex

Age vs. Max Heart Rate thalach

Heart disease frequency chest pain type

5. Modelling

Now we have got our data into train and test size, it's time to build the model

We'll train it(find the patterns) on the training set.

And we'll test it (use th patterns) in the test set.

We're going to try 3 different machine learning models:

  1. Logistic Regression
  2. K-Nearest Neighbours Classifier
  3. RandomForest Classifier

Model Comparision

Beautiful! We can't really see it from the graph but looking at the dictionary, the LogisticRegression() model performs best.

Since you've found the best model. Let's take it to the boss and show her what we've found.

You: I've found it!

Her: Nice one! What did you find?

You: The best algorithm for prediting heart disease is a LogisticRegrssion!

Her: Excellent. I'm surprised the hyperparameter tuning is finished by now.

You: wonders what hyperparameter tuning is

You: Ummm yeah, me too, it went pretty quick.

Her: I'm very proud, how about you put together a classification report to show the team, and be sure to include a confusion matrix, and the cross-validated precision, recall and F1 scores. I'd also be curious to see what features are most important. Oh and don't forget to include a ROC curve.

You: asks self, "what are those???"

You: Of course! I'll have to you by tomorrow.

Alright, there were a few words in there which could sound made up to someone who's not a budding data scientist like yourself. But being the budding data scientist you are, you know data scientists make up words all the time.

Let's briefly go through each before we see them in action.

Hyperparameter tuning and cross-validation

To cook your favourite dish, you know to set the oven to 180 degrees and turn the grill on. But when your roommate cooks their favourite dish, they set use 200 degrees and the fan-forced mode. Same oven, different settings, different outcomes.

The same can be done for machine learning algorithms. You can use the same algorithms but change the settings (hyperparameters) and get different results.

But just like turning the oven up too high can burn your food, the same can happen for machine learning algorithms. You change the settings and it works so well, it overfits (does too well) the data.

We're looking for the goldilocks model. One which does well on our dataset but also does well on unseen examples.

To test different hyperparameters, you could use a validation set but since we don't have much data, we'll use cross-validation.

The most common type of cross-validation is k-fold. It involves splitting your data into k-fold's and then testing a model on each. For example, let's say we had 5 folds (k = 5). This what it might look like.
Normal train and test split versus 5-fold cross-validation

We'll be using this setup to tune the hyperparameters of some of our models and then evaluate them. We'll also get a few more metrics like precision, recall, F1-score and ROC at the same time.

Here's the game plan:

  1. Tune model hyperparameters, see which performs best
  2. Perform cross-validation
  3. Plot ROC curves
  4. Make a confusion matrix
  5. Get precision, recall and F1-score metrics
  6. Find the most important model features

Hyperpaatameter

Hyperparameter tuning with RandomizedSearchCV

We are going to tune :

Now we've got hyperparameter grid setup foe each of our models, Let's tune them using RandomizedSearchCV...

Excellent! Tuning the hyperparameters for each model saw a slight performance boost in both the RandomForestClassifier and LogisticRegression.

This is akin to tuning the settings on your oven and getting it to cook your favourite dish just right.

But since LogisticRegression is pulling out in front, we'll try tuning it further with GridSearchCV.

Tuning a model with GridSearchCV

The difference between RandomizedSearchCV and GridSearchCV is where RandomizedSearchCV searches over a grid of hyperparameters performing n_iter combinations, GridSearchCV will test every single possible combination.

In short:

Let's see it in action.

In this case, we get the same results as before since our grid only has a maximum of 20 different hyperparameter combinations.

Note: If there are a large amount of hyperparameters combinations in your grid, GridSearchCV may take a long time to try them all out. This is why it's a good idea to start with RandomizedSearchCV, try a certain amount of combinations and then use GridSearchCV to refine them.

Evaluating a classification model, beyond accuracy

Now we've got a tuned model, let's get some of the metrics we discussed before.

We want:

Luckily, Scikit-Learn has these all built-in.

To access them, we'll have to use our model to make predictions on the test set. You can make predictions by calling predict() on a trained model and passing it the data you'd like to predict on.

We'll make predictions on the test data.

Since we've got our prediction values we can find the metrics we want.

Let's start with the ROC curve and AUC scores.

ROC Curve and AUC Scores

What's a ROC curve?

It's a way of understanding how your model is performing by comparing the true positive rate to the false positive rate.

In our case...

To get an appropriate example in a real-world problem, consider a diagnostic test that seeks to determine whether a person has a certain disease. A false positive in this case occurs when the person tests positive, but does not actually have the disease. A false negative, on the other hand, occurs when the person tests negative, suggesting they are healthy, when they actually do have the disease.

Scikit-Learn implements a function plot_roc_curve which can help us create a ROC curve as well as calculate the area under the curve (AUC) metric.

Reading the documentation on the plot_roc_curve function we can see it takes (estimator, X, y) as inputs. Where estiamator is a fitted machine learning model and X and y are the data you'd like to test it on.

In our case, we'll use the GridSearchCV version of our LogisticRegression estimator, gs_log_reg as well as the test data, X_test and y_test.

This is great, our model does far better than guessing which would be a line going from the bottom left corner to the top right corner, AUC = 0.5. But a perfect model would achieve an AUC score of 1.0, so there's still room for improvement.

Let's move onto the next evaluation request, a confusion matrix.

Confusion matrix

A confusion matrix is a visual way to show where your model made the right predictions and where it made the wrong predictions (or in other words, got confused).

Scikit-Learn allows us to create a confusion matrix using confusion_matrix() and passing it the true labels and predicted labels.

As you can see, Scikit-Learn's built-in confusion matrix is a bit bland. For a presentation you'd probably want to make it visual.

Let's create a function which uses Seaborn's heatmap() for doing so.

Beautiful! That looks much better.

You can see the model gets confused (predicts the wrong label) relatively the same across both classes. In essence, there are 4 occasaions where the model predicted 0 when it should've been 1 (false negative) and 3 occasions where the model predicted 1 instead of 0 (false positive).

Classification report

We can make a classification report using classification_report() and passing it the true labels as well as our models predicted labels.

A classification report will also give us information of the precision and recall of our model for each class.

What's going on here?

Let's get a refresh.

Ok, now we've got a few deeper insights on our model. But these were all calculated using a single training and test set.

What we'll do to make them more solid is calculate them using cross-validation.

How?

We'll take the best model along with the best hyperparameters and use cross_val_score() along with various scoring parameter values.

cross_val_score() works by taking an estimator (machine learning model) along with data and labels. It then evaluates the machine learning model on the data and labels using cross-validation and a defined scoring parameter.

Let's remind ourselves of the best hyperparameters and then see them in action.

Okay, we've got cross validated metrics, now what?

Let's visualize them.

Great! This looks like something we could share. An extension might be adding the metrics on top of each bar so someone can quickly tell what they were.

What now?

The final thing to check off the list of our model evaluation techniques is feature importance.

Feature importance

Feature importance is another way of asking, "which features contributing most to the outcomes of the model?"

Or for our problem, trying to predict heart disease using a patient's medical characterisitcs, which charateristics contribute most to a model predicting whether someone has heart disease or not?

Unlike some of the other functions we've seen, because how each model finds patterns in data is slightly different, how a model judges how important those patterns are is different as well. This means for each model, there's a slightly different way of finding which features were most important.

You can usually find an example via the Scikit-Learn documentation or via searching for something like "[MODEL TYPE] feature importance", such as, "random forest feature importance".

Since we're using LogisticRegression, we'll look at one way we can calculate feature importance for it.

To do so, we'll use the coef_ attribute. Looking at the Scikit-Learn documentation for LogisticRegression, the coef_ attribute is the coefficient of the features in the decision function.

We can access the coef_ attribute after we've fit an instance of LogisticRegression.

Looking at this it might not make much sense. But these values are how much each feature contributes to how a model makes a decision on whether patterns in a sample of patients health data leans more towards having heart disease or not.

Even knowing this, in it's current form, this coef_ array still doesn't mean much. But it will if we combine it with the columns (features) of our dataframe.

Now we've match the feature coefficients to different features, let's visualize them.

You'll notice some are negative and some are positive.

The larger the value (bigger bar), the more the feature contributes to the models decision.

If the value is negative, it means there's a negative correlation. And vice versa for positive values.

For example, the sex attribute has a negative value of -0.904, which means as the value for sex increases, the target value decreases.

We can see this by comparing the sex column to the target column.

You can see, when sex is 0 (female), there are almost 3 times as many (72 vs. 24) people with heart disease (target = 1) than without.

And then as sex increases to 1 (male), the ratio goes down to almost 1 to 1 (114 vs. 93) of people who have heart disease and who don't.

What does this mean?

It means the model has found a pattern which reflects the data. Looking at these figures and this specific dataset, it seems if the patient is female, they're more likely to have heart disease.

How about a positive correlation?

Looking back the data dictionary, we see slope is the "slope of the peak exercise ST segment" where:

According to the model, there's a positive correlation of 0.470, not as strong as sex and target but still more than 0.

This positive correlation means our model is picking up the pattern that as slope increases, so does the target value.

Is this true?

When you look at the contrast (pd.crosstab(df["slope"], df["target"]) it is. As slope goes up, so does target.

What can you do with this information?

This is something you might want to talk to a subject matter expert about. They may be interested in seeing where machine learning model is finding the most patterns (highest correlation) as well as where it's not (lowest correlation).

Doing this has a few benefits:

  1. Finding out more - If some of the correlations and feature importances are confusing, a subject matter expert may be able to shed some light on the situation and help you figure out more.
  2. Redirecting efforts - If some features offer far more value than others, this may change how you collect data for different problems. See point 3.
  3. Less but better - Similar to above, if some features are offering far more value than others, you could reduce the number of features your model tries to find patterns in as well as improve the ones which offer the most. This could potentially lead to saving on computation, by having a model find patterns across less features, whilst still achieving the same performance levels.

6. Experimentation

Well we've completed all the metrics your boss requested. You should be able to put together a great report containing a confusion matrix, a handful of cross-valdated metrics such as precision, recall and F1 as well as which features contribute most to the model making a decision.

But after all this you might be wondering where step 6 in the framework is, experimentation.

Well the secret here is, as you might've guessed, the whole thing is experimentation.

From trying different models, to tuning different models to figuring out which hyperparameters were best.

What we've worked through so far has been a series of experiments.

And the truth is, we could keep going. But of course, things can't go on forever.

So by this stage, after trying a few different things, we'd ask ourselves did we meet the evaluation metric?

Remember we defined one in step 3.

If we can reach 95% accuracy at predicting whether or not a patient has heart disease during the proof of concept, we'll pursure this project.

In this case, we didn't. The highest accuracy our model achieved was below 90%.

What next?

You might be wondering, what happens when the evaluation metric doesn't get hit?

Is everything we've done wasted?

No.

It means we know what doesn't work. In this case, we know the current model we're using (a tuned version of LogisticRegression) along with our specific data set doesn't hit the target we set ourselves.

This is where step 6 comes into its own.

A good next step would be to discuss with your team or research on your own different options of going forward.

The key here is to remember, your biggest restriction will be time. Hence, why it's paramount to minimise your times between experiments.

The more you try, the more you figure out what doesn't work, the more you'll start to get a hang of what does.